How to implement a 3-bit Adder in VHDL (For an Altera FPGA utilizing a 7-segment display)

This page covers some of the design process and finishes with VHDL code, scroll down for VHDL.

Adders - Introduction

Addition is arguably one of the most important arithmetic operations used in the world we live in. Being one of the first mathematical operations ever conceived, it is a fundamental problem in everyday life. Adders are incredibly important in digital electronics and computers. Modern computers perform millions of addition operations a second. Adders are extremely important not only in the ALU but also in other parts of the processor where memory addresses must be calculated.
The value of the adder circuit in modern electronics is paramount.

Building Blocks of the 3-bit Adder

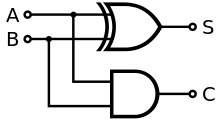
Half Adder:

The half adder adds two single binary digits A and B. It has two outputs, sum (S) and carry (C). A carry bit is required to 'carry' the overflow product present in some addition cases.

Full Adder:

A full adder adds binary numbers and calculates both for values carried in, as well as carried out. A one-bit full adder adds three one-bit numbers, often written as A, B, and Cin; A and B are the operands, and Cin is a bit carried in from the previous less significant stage. Just like the half adder, it produces two output bits Cout and S.

With the case of the Full Adder, we see that the last OR gate can actually be replaced with an XOR gate without affecting the working of the circuit. This fact may be helpful in determining the resources needed for our circuit at a later stage as we can completely get rid of OR gates.

Putting it all together:

By laying the 1 bit full adders in an array, we can simulate the addition of binary numbers. Since the first adder of the circuit does not take a carry in input, we can substitute it with a half-adder to cut down on resources and number of gates required. The block diagrams below actually represent the circuits drawn above.

Implementation in VHDL (For Altera DE1 using Altera's Pin-out plan) :

Pin mapping for Altera Quartus - click here.

library ieee;
use ieee.std_logic_1164.all;

entity ERS220eg is
port (
  LEDG : OUT std_logic_vector(7 DOWNTO 0);
  LEDR : OUT std_logic_vector(9 DOWNTO 0);
  SW : IN std_logic_vector(9 DOWNTO 0);
  HEX0 : OUT std_logic_vector(6 DOWNTO 0);
  HEX1 : OUT std_logic_vector(6 DOWNTO 0);
  HEX2 : OUT std_logic_vector(6 DOWNTO 0);
  HEX3 : OUT std_logic_vector(6 DOWNTO 0)
  
  );
  
end ERS220eg;

architecture behave of ERS220eg is
begin
 
 LEDG(7) <= SW(9);

 PROCESS(SW(9)) is
 
  variable c_zero : std_logic := '0';
  variable c_one : std_logic := '0';
  variable c_two : std_logic := '0';
  variable ans : std_logic_vector(3 DOWNTO 0);
  variable a,b : std_logic_vector(2 DOWNTO 0);
  
  begin
  
  LEDR(9) <= SW(9);
  
  if (SW(9) = '1') then
  
   HEX0 <= (others => '0');
   HEX1 <= (others => '1');
  
 --  LEDG(0) <= SW(0) AND SW(1);
 --  LEDG(1) <= SW(0) OR SW(1);
 --  LEDG(2) <= SW(0) XOR SW(1);

   LEDR(5 DOWNTO 0) <= SW(5 DOWNTO 0);

   -- LEDG0 is D0 which is carry out from half adder:
   -- LSB:
   
   ANS(0) := SW(0) XOR SW(3);
   
   c_zero := SW(0) AND SW(3);
   
   -- Second bit - first full adder
   
   ANS(1) := c_zero XOR (SW(1) XOR SW(4));
   c_one := (SW(1) AND SW(4)) XOR (c_zero AND (SW(1) XOR SW(4)));
   
   -- Third bit - second full adder
   
   ANS(2) := c_one XOR (SW(2) XOR SW(5));
   c_two := (SW(2) AND SW(5)) XOR (c_one AND (SW(2) XOR SW(5)));
   
   -- resultant carry
   ANS(3) := c_two;
   
   LEDG(3 DOWNTO 0) <= ANS(3 DOWNTO 0);
   
   -- 7 seg:
   
   a := SW(2 DOWNTO 0);
   b := SW(5 DOWNTO 3);
   
   
   CASE b IS
    WHEN "000"=>HEX3<="1000000";
    WHEN "001"=>HEX3<="1111001";
    WHEN "010"=>HEX3<="0100100";
    WHEN "011"=>HEX3<="0110000";
    WHEN "100"=>HEX3<="0011001";
    WHEN "101"=>HEX3<="0010010";
    WHEN "110"=>HEX3<="0000010";
    WHEN "111"=>HEX3<="1111000";
    WHEN OTHERS=>HEX3<="1111111";
   END CASE;
   
   CASE a IS
    WHEN "000"=>HEX2<="1000000";
    WHEN "001"=>HEX2<="1111001";
    WHEN "010"=>HEX2<="0100100";
    WHEN "011"=>HEX2<="0110000";
    WHEN "100"=>HEX2<="0011001";
    WHEN "101"=>HEX2<="0010010";
    WHEN "110"=>HEX2<="0000010";
    WHEN "111"=>HEX2<="1111000";
    WHEN OTHERS=>HEX2<="1111111";
   END CASE;
   
   HEX1 <= "0110111";
   
   
   CASE ANS IS
    WHEN "0000"=>HEX0<="1000000";
    WHEN "0001"=>HEX0<="1111001";
    WHEN "0010"=>HEX0<="0100100";
    WHEN "0011"=>HEX0<="0110000";
    WHEN "0100"=>HEX0<="0011001";
    WHEN "0101"=>HEX0<="0010010";
    WHEN "0110"=>HEX0<="0000010";
    WHEN "0111"=>HEX0<="1111000";
    WHEN "1000"=>HEX0<="0000000";
    WHEN "1001"=>HEX0<="0011000";
    WHEN "1010"=>HEX0<="0001000"; -- A
    WHEN "1011"=>HEX0<="0000011"; -- B
    WHEN "1100"=>HEX0<="0100111"; -- C
    WHEN "1101"=>HEX0<="0100001"; -- d
    WHEN "1110"=>HEX0<="0000110"; -- e
    WHEN OTHERS=>HEX0<="1111111";
   END CASE;
   
  else
  
   HEX0 <= (others => '1');
   HEX1 <= (others => '1');
   HEX2 <= (others => '1');
   HEX3 <= (others => '1');
  
   LEDG(6 DOWNTO 0) <= (others => '0');
   LEDR(6 DOWNTO 0) <= (others => '0');
  
  end if;
 end process;
end behave;